We developed a $\Theta(n^3)$ algorithm, which is Floyd Algorithm, for determining the shortest paths from each vertex to all other vertices in a weighted, directed graph. If we wanted to know only the shortest paths from one particular vertex to all the others, that algorithm would be overkill. Therefore, we will use the greedy approach to develop a $\Theta(n^2)$ algorithm for this problem (called the Single Source Shortest Paths problem). This algorithm is due to Dijkstra (1959).
앞서 동적계획법으로 살펴 본 플로이드 알고리즘 역시 최단경로 문제와 관련된 해법을 제시해준다. 플로이드 알고리즘의 경우, 그래프상의 각 정점에서 다른 모든 정점으로 가는 최단 경로를 제시해 준다.
하나의 특정 정점에서 다른 정점으로 가는 최단경로를 구하기 위해 플로이드 알고리즘을 사용하는 것은 과잉이다. 이 경우 탐욕적 접근법으로 설계된 다익스트라 알고리즘을 사용하여 문제를 해결하면 된다.
Example Determine the shortest paths from $v_1$ to all other vertices in a weighted, directed graph.
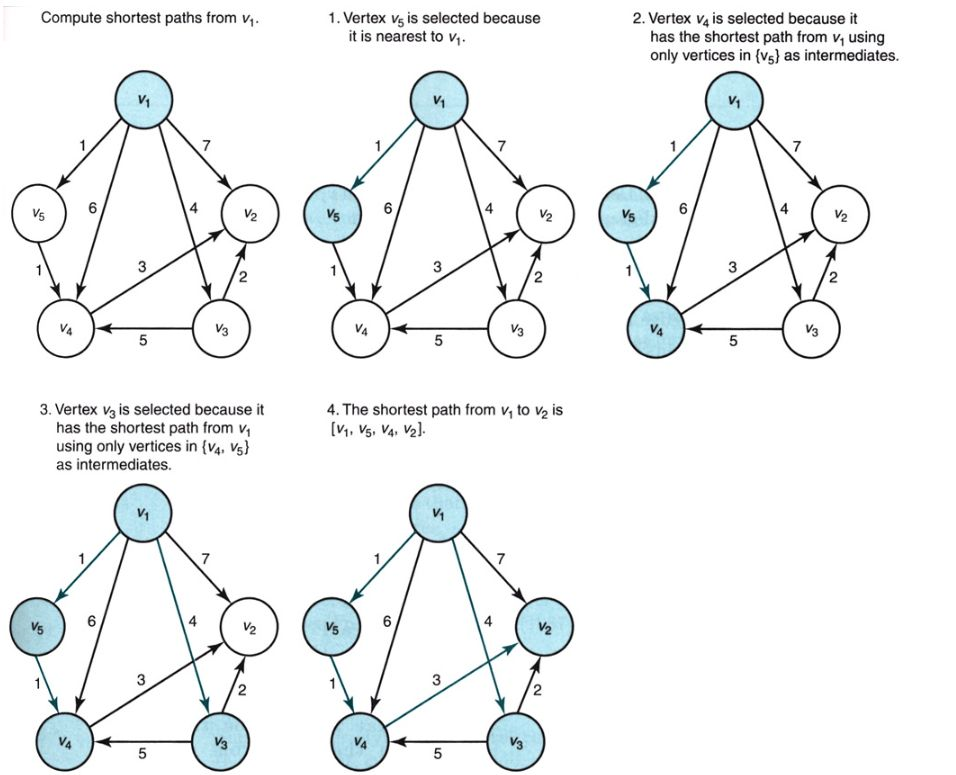
Init. $v_1$에서 다른 정점들로 가는 최단경로를 계산하고, 시작정점인 $v_1$이 먼저 선택된다.
Step 1 $v_1$에서 가장 가까운 정점인 $v_5$가 선택된다.
Step 2 $v_1$으로부터 {$v_5$}를 통해서 갈 수 있는 다음의 가장 가까운 정점은 $v_4$이므로, $v_4$가 선택된다.
Step 3 $v_1$으로부터 {$v_4$, $v_5$}를 통해서 갈 수 있는 다음의 가장 가까운 정점은 $v_3$이므로, $v_3$가 선택된다.
Step 4 $v_1$으로부터 {$v_3$, $v_4$, $v_5$}를 통해서 갈 수 있는 다음의 가장 가까운 정점은 $v_2$이다.
| 최단경로확정여부 | $v_1$ $\rightarrow$ $v_1$ | $v_1$ $\rightarrow$ $v_2$ | $v_1$ $\rightarrow$ $v_3$ | $v_1$ $\rightarrow$ $v_4$ | $v_1$ $\rightarrow$ $v_5$ |
|---|---|---|---|---|---|
| Step 1 | Y | N | N | N | Y |
| Step 2 | Y | N | N | Y | Y |
| Step 3 | Y | N | Y | Y | Y |
| Step 4 | Y | Y | Y | Y | Y |
The Dijkstra’s Algorithm for Single-Source Shortest Paths
Algorithm Design
We initialize a set Y to contain only the vertex whose shortest paths are to be determined (the vertex is $v_1$). We initialize a set F of edges to being empty. First we choose a vertex $v$ that is nearest to $v_1$, add it to Y, and add the edge <$v_1$, $v$> to F. That edge is clearly a shortest path from $v_1$ to $v$. Next we check the paths from $v_1$ to the vertices in V - Y that allow only vertices in Y as intermediate vertices. A shortest of these paths is a shortest path. The vertex at the end of such a path is added to Y, and the edge (on the path) that touches that vertex is added to F. This procedure is continued until Y equals V, the set of all vertices. At this point, F contains the edges in shortest paths.
This algorithm is very similar to Prim’s algorithm. The difference is that instead of the arrays nearest and distance, we have arrays touch and length, where for i = 2, …, n.
touch[i] = index of vertex $v$ in Y such that the edge <$v$, $v_i$> is the last edge on the current shortest path from $v_1$ to $v_i$ using only vertices in Y as intermediates.
length[i] = length of the current shortest path from $v_1$ to $v_i$ using only vertices in Y as intermediates.
[용어정의]
| 구분 | 설명 |
|---|---|
| G=(V,E) | 모든 정점들의 집합 V와 모든 이음선들의 집합 E로 구성된 그래프 G. |
| Y | 시작정점으로부터 최단경로가 이미 결정된 정점들의 집합이다. |
| F | Y의 정점들을 최단경로로 연결시키는 이음선들의 집합이다. |
| touch[i] | Y에 속한 정점 $v$의 인덱스이다. |
| length[i] | Y에 속한 정점만을 통해서 $v_i$로 가는 현재까지의 최단경로 길이이다. |
[다익스트라 알고리즘 초기화 로직]
Y는 $v_1$(시작정점)만 포함하도록, F는 어떤 이음선도 포함하지 않도록 초기화시킨다.
touch[i]는 시작정점인 $v_1$을 가리키는 1로 값을 초기화한다. 즉, touch[2], touch[3], …, touch[k] 값 모두 1이다. length[i] 값은 본래 시작정점에서 다른 정점으로 가는 경로의 길이로 초기화한다 (초기화 시점에서 Y에 속한 정점은 시작정점인 $v_1$하나)
[다익스트라 알고리즘 메인 로직]
$v_1$에서 가장 가까운 정점 $v$를 선택하여 Y에 추가하고, $v_1$과 $v$를 연결하는 이음선은 F에 추가한다. 이 이음선은 분명 $v_1$에서 $v$까지의 최단경로이다. 다음으로 $v_1$에서 Y에 속해있는 정점들을 통해서 갈 수 있는 V - Y에 속한 정점들까지의 거리를 점검한다. 이 경로 중 가장 짧은 경로는 최단경로이므로, 해당 정점을 Y에 추가하고 그 정점과 연결되는 경로상의 이음선을 F에 추가한다. 이 과정을 Y가 모든 정점들의 집합 V와 같아질때까지 반복 수행한다.
| min | vnear | Y추가 | F추가 | length [2][3][4][5] |
touch [2][3][4][5] |
|
|---|---|---|---|---|---|---|
| Init. | - | 1 | $v_1$ | ∅ | 7 4 6 1 | 1 1 1 1 |
| Step 1 | 1 | 5 | $v_5$ | <$v_1$,$v_5$> | 7 4 2 -1 | 1 1 5 1 |
| Step 2 | 2 | 4 | $v_4$ | <$v_5$,$v_4$> | 5 4 -1 -1 | 4 1 5 1 |
| Step 3 | 4 | 3 | $v_3$ | <$v_1$,$v_3$> | 5 -1 -1 -1 | 4 1 5 1 |
| Step 4 | 5 | 2 | $v_2$ | <$v_4$,$v_2$> | -1 -1 -1 -1 | 4 1 5 1 |
시작정점을 포함시키지 않아도 되므로 총 n-1번의 루프를 수행한다. 메인루프에는 두 개의 for문이 존재하는데, 첫번째 for문은 length[i]의 값들 중에서 가장 작은 값을 찾아 기록한다 (vnear). 다른 하나의 for문은 새로 추가된 정점을 현재까지의 중간정점에 포함시켜, 이를 이용해서 갈 수 있는 경로가 현재 경로의 값보다 작다면 length[i]와 touch[i]의 값을 갱신한다.
이 과정을 n-1번 반복수행하면 한 특정 정점에서 다른 정점으로 가는 최단경로를 구할 수 있다. 책에서는 시작정점을 $v_1$으로 한정짓고 있지만, 융통성 있는 프로그램을 위해 시작정점을 선택할 수 있도록 프로그램을 구현했다.
Pseudo Code
void dijkstra(int n, const number W[ ][ ], set_of_edges& F) |
Source Code
// File: dijkstra.h |
// File: dijkstra.cpp |
// File: shorttest.cpp |
Time Complexity Analysis
Basic operation
- There are two loops, each with n-1 iterations, inside the repeat loop. Executing the instructions inside each of them can be considered to be doing the basic operation once.
Input size
- n, the number of vertices.
Every-Case Time Complexity
- $ T(n) = (n-1)2(n-1) = 2(n-1)^2 \in \Theta(n^2) $
Optimality Proof
We use a proof by contradiction. But first, we assert the following.
Lemma
Lemma 1 Shortest paths are composed of shortest paths.
The proof of this is based on the notion that if there was a shorter path than any sub-path, then the shorter path should replace that sub-path to make the whole path shorter.
최단경로를 구성하는 부분경로들 역시 최단경로이다.
Lemma 2 If s $\rightarrow$ … $\rightarrow$ u $\rightarrow$ v is a shortest path from s to v, then after u has been added to Y and we check paths from u to vertices in V - Y that allow only vertices in Y as intermediate vertices. Therefore, length[v] = δ(s,v) and length[v] is not changed thereafter.
// check paths from u to vertices in V - Y that allow only vertices |
s에서 v로가는 최단경로가 s $\rightarrow$ … $\rightarrow$ u $\rightarrow$ v일 때, 정점 u가 Y에 추가되면서 length[v]를 더 짧은 거리로 갱신할 수 있는지 점검하므로 결국 length[v] = δ(s,v)가 된다. length[v] 값은 그 이후로 변하지 않는다.
Proof by contradiction
Proof For each vertex u ∈ V, it follows from the fact that at all times length[u] $\ge$ δ(s,u). After running Dijkstra’s algorithm, we assert that length[u] = δ(s,u).
다익스트라 알고리즘이 찾아낸 최단경로의 정확성을 검증한다. δ(s,u)는 시작정점 s에서 u까지의 최단경로를 의미하므로, 알고리즘 수행 후 모든 정점 u에 대해 length[u] = δ(s, u)가 성립함을 보이면 된다.
증명을 위해 귀류법(proof by contradiction)을 사용한다. 귀류법이란 어떤 명제를 반대로 가정했을 때, 모순을 이끌어내어 가정이 거짓임을 증명하는 방법이다.
Hypothesis Suppose that u is the first vertex added to Y for which length[u] ≠ δ(s,u). We note:
- u cannot be s, because length[s] = 0.
- There must be a path from s to u. If there were not, length[u] would be infinity.
- Since there is a path, there must be a shortest path.
Y(최단경로가 결정된 정점들의 집합)에 추가되는 첫번째 정점이 u일 때, 다익스트라 알고리즘이 정점 u에 대해 최단경로를 산출하지 못한다고 가정하자. (length[u] ≠ δ(s,u)) 바꿔 말하면 알고리즘이 산출한 최단경로보다 더 좋은 경로가 존재함을 의미한다.
먼저 u는 시작정점일 수 없다. 시작정점은 length[s] = δ(s,s) = 0 이기 때문이다.
또한, s $\rightarrow$ u 까지의 경로는 반드시 존재한다. 그렇지 않으면 length[u]는 무한대 값이므로, Y에 속하는 첫번째 정점으로 u가 선택될 수 없다.
정리하면 s $\rightarrow$ u 까지의 최단경로가 존재하며, length[u] ≠ δ(s,u)이므로 현재까지 찾은 최단경로보다 더 짧은 최단경로가 존재한다.
Let s $\rightarrow$ v $\rightarrow$ w $\rightarrow$ u be the shortest path from s to u. Where v is within Y and w is the first vertex not within Y. When v was inserted into Y, length[v] = δ(s,v) (since we hypothesise that u was the first vertex for which this was not true). Edge (v,w) was relaxed at that time, so that
$$
\begin{align}
length[w] &= δ(s,w) \\
&\le δ(s,u) \\
&\le length[u] \tag{due to $w$ $\rightarrow$ $u$}
\end{align}
$$
그 최단경로를 s $\rightarrow$ v $\rightarrow$ w $\rightarrow$ u라고 하면, v는 Y에 속한 임의의 정점이고 w는 V-Y에 속한 임의의 정점이다. 그리고 보조정리에 따라 length[v] = δ(s,v)이며, v를 통해 w로가는 length[w] 값 역시 갱신된 상태다.
사실 이 최단경로는 참일 수 없다. 첫번째로 선택된 정점이 u인데 Y에 이미 v라는 정점이 존재하기 때문이다. 하지만 length[u] = δ(s,u)를 보이기 위해 증명을 계속 진행한다.
Now both w and u were in V-Y when u was chosen, so
$$
length[u] \le length[w]
$$
w, u 둘다 V-Y에 속하는 정점이다. 여기서 u를 첫번째 정점으로 선택했다는 것은 시작정점으로부터 최단거리를 가지는 정점이 u라는 뜻이다.
Thus the two inequalities must be equalities,
$$
\underbrace{length[w] = δ(s,w) = δ(s,u) = length[u]}_{\text{length[w] $\le$ length[u] & length[u] $\le$ length[w]}}
$$
So length[u] = δ(s,u) contradicting our hypothesis.
Thus when each vertex u ∈ V was inserted to Y, length[u] = δ(s,u).
Therefore, by the proof of contradiction, Dijkstra’s algorithm always produces Shortest Paths.
두 부등식에 의해 length[u] = δ(s,u)가 되므로, 다익스트라 알고리즘이 정점 u에 대해 최단경로를 산출하지 못한다는 가정에 모순이 생긴다. 그러므로 각 정점 u가 Y에 추가되면 length [u] = δ(s, u)이며, 다익스트라 알고리즘에서 계산된 Length[u]는 s에서 u까지의 최단경로이다.
Greedy Approach Exercises
Use Dijkstra’s algorithm to find the shortest paths from the vertex $v_4$ to all the other vertices of the below graph.
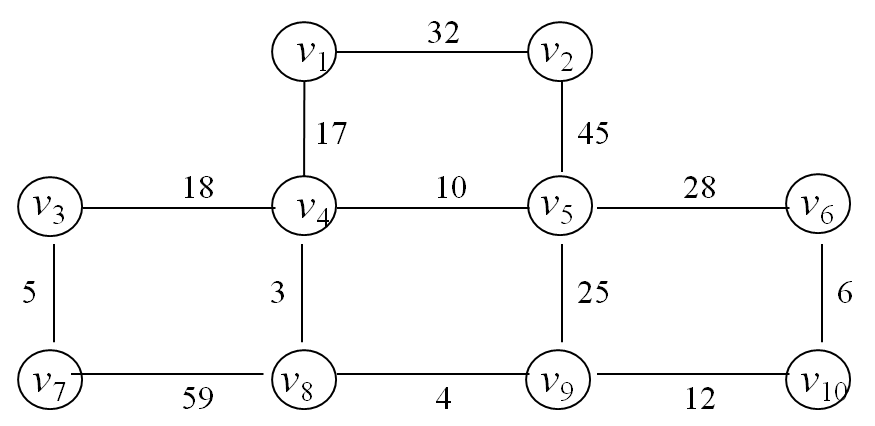
/* adjacency matrix for the above graph */ |